Information Design

Please see the conference version of this work for details.

Oct 13, 2025

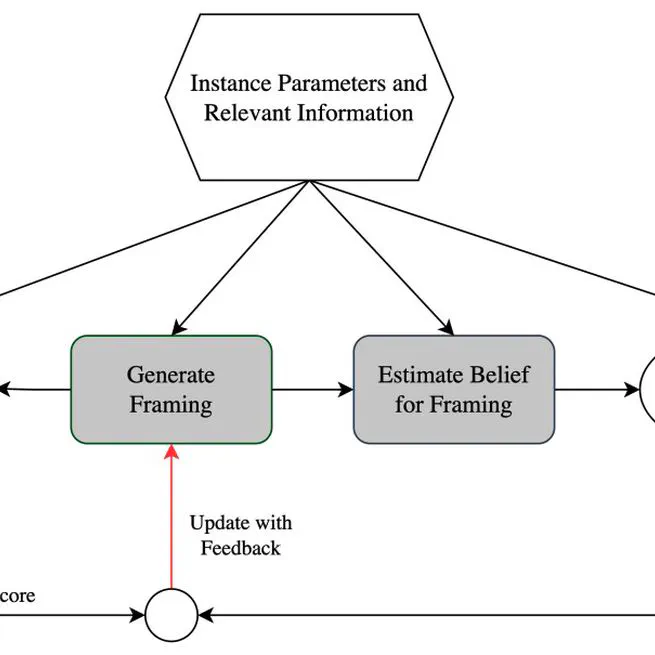
Information design is typically studied through the lens of Bayesian signaling, where signals shape beliefs based on their correlation with the true state of the world. However, Behavioral Economics and Psychology emphasize that human decision-making is more complex and can depend on how information is framed. This paper formalizes a language-based notion of framing and bridges this to the popular Bayesian-persuasion model. We model framing as a possibly non-Bayesian, linguistic way to influence a receiver’s belief, while a signaling (or recommendation) scheme can further refine this belief in the classic Bayesian way. A key challenge in systematically optimizing in this framework is the vast space of possible framings and the difficulty of predicting their effects on receivers. Based on growing evidence that Large Language Models (LLMs) can effectively serve as proxies for human behavior, we formulate a theoretical model based on access to a framing-to-belief oracle. This model then enables us to precisely characterize when solely optimizing framing or jointly optimizing framing and signaling is tractable. We substantiate our theoretical analysis with an empirical algorithm that leverages LLMs to (1) approximate the framing-to-belief oracle, and (2) optimize over language space using a hill-climbing method. We apply this to two marketing-inspired case studies and validate the effectiveness through analytical and human evaluation.

Sep 29, 2025

Aug 19, 2025

Classic principal-agent problems such as Stackelberg games, contract design, and Bayesian persuasion, often assume that the agent is able to best respond to the principal’s committed strategy. We study repeated generalized principal-agent problems under the assumption that the principal does not have commitment power and the agent uses algorithms to learn to respond to the principal. We reduce this problem to a one-shot generalized principal-agent problem where the agent approximately best responds. Using this reduction, we show that: (1) If the agent uses contextual no-regret learning algorithms with regret $\mathrm{Reg}(T)$, then the principal can guarantee utility at least $U^* - \Theta\big(\sqrt{\tfrac{\mathrm{Reg}(T)}{T}}\big)$, where $U^*$ is the principal’s optimal utility in the classic model with a best-responding agent. (2) If the agent uses contextual no-swap-regret learning algorithms with swap-regret $\mathrm{SReg}(T)$, then the principal cannot obtain utility more than $U^* + O(\frac{\mathrm{SReg(T)}}{T})$. But (3) if the agent uses mean-based learning algorithms (which can be no-regret but not no-swap-regret), then the principal can sometimes do significantly better than $U^*$. These results not only refine previous results in Stackelberg games and contract design, but also lead to new results for Bayesian persuasion with a learning agent and all generalized principal-agent problems where the agent does not have private information.

Apr 24, 2025

Jan 5, 2025

Dec 1, 2024

Jul 1, 2024